在游戏开发中，需要使用到向量，三角函数之类的知识。先学会里面的概念，后续应用才会容易制作。

3d数学

1.笛卡尔坐标系（Cartesian）

2d坐标系：x,y

3d坐标系：x,y,z

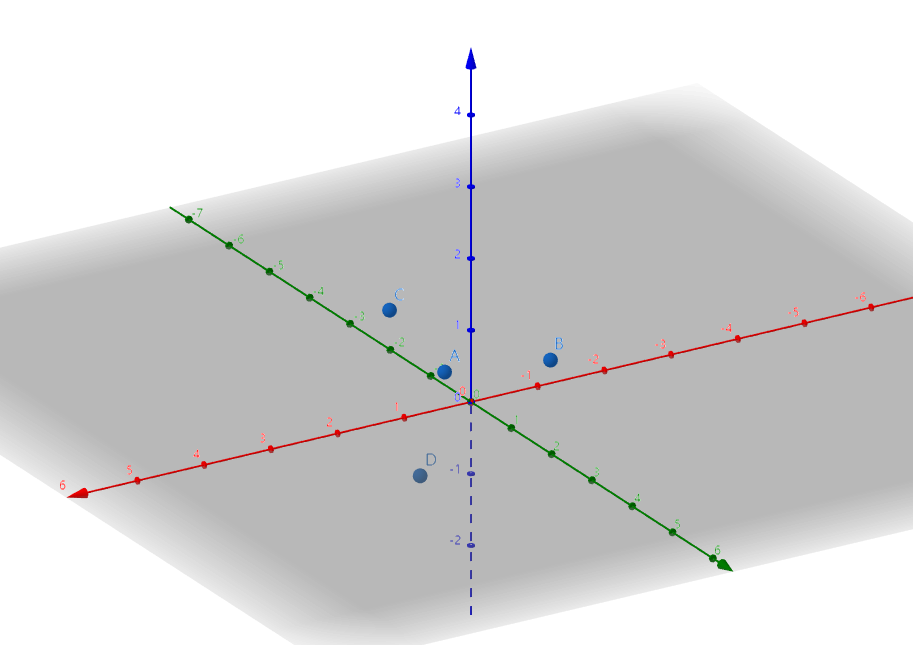
在3d坐标系里面有左手坐标系和右手坐标系。这个可能对人来说有直观认知上的区别，其实是不相悖。

右手坐标系

左手坐标系

附带：

极坐标系（polar coordinates）是指在平面内由极点、极轴和极径组成的坐标系。在平面上取定一点O，称为极点。从O出发引一条射线Ox，称为极轴。再取定一个单位长度，通常规定角度取逆时针方向为正。这样，平面上任一点P的位置就可以用线段OP的长度ρ以及从Ox到OP的角度θ来确定，有序数对（ρ，θ）就称为P点的极坐标，记为P（ρ，θ）；ρ称为P点的极径，θ称为P点的极角。

极坐标系用于定位和导航。极坐标通常被用于导航，作为旅行的目的地或方向可以作为从所考虑的物体的距离和角度。

2.三角学

这块的知识属于初等函数。初等函数包含的有：

幂函数、指数函数、对数函数、三角函数、反三角函数、有理运算（加减乘除，有理数次乘方、有理数次开放）、有限次函数复合。

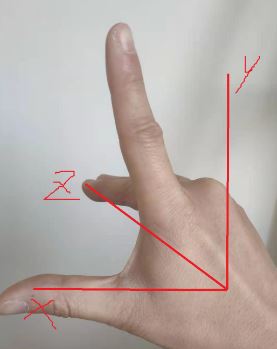
1.直角三角形三角函数概念

• 对边 Opposite（opp） y
• 邻边 Adjacent（adj） x
• 斜边 Hypotenuse（hyp） r

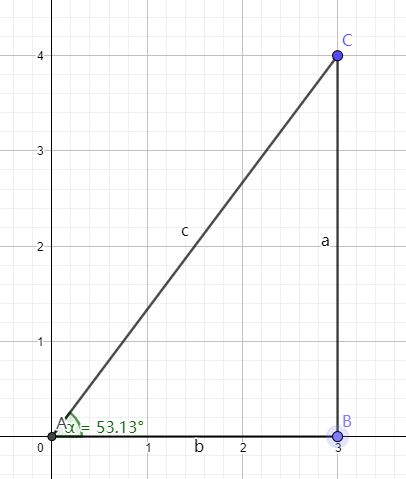
勾股定理（毕达哥拉斯定理）

$r=\sqrt{x^2+y^2}$

$5=\sqrt{3^2+4^2}$

$∠A 为\theta$

余弦 cosine

邻边比斜边。

$cos(\theta) = \frac{x}{r}$

正弦 sine

对边比斜边。

$sin(\theta) = \frac{y}{r}$

正弦余弦背诵的时候，按照字母排序，x < y ，cos < sin。

割线 secant

$\sec(\theta)=\frac{1}{\cos(\theta)}$

$\sec(\theta)=\frac{r}{x}$

余割 cosecant

$\csc(\theta)=\frac{1}{\sin(\theta)}$

$\csc(\theta)=\frac{r}{y}$

切线 tangent

对边比邻边。

$\tan(\theta)=\frac{\sin(\theta)}{\cos(\theta)}$

$\tan(\theta) = \frac{y}{x}$

余切 cotangent

邻边比对边。

$\cot(\theta) = \frac{1}{\tan(\theta)}=\frac{\cos(\theta)}{sin(\theta)}$

$\cot(\theta) = \frac{x}{y}$

反切线函数

反切线函数的反函数 arctangent

$\arctan(\tan(\theta)) = \theta$

2.角度弧度

半径为1的园，全弧长为2$\pi$r。

$radian=degree*(\pi/180)$

$degree = radian*(180/\pi)$

角度是两条线段的夹角，弧度是两条线段和园相交的点，在圆弧上走过的距离。

角度使用360°，原因来自于日历。波斯日历就是360天。360能被整除的数字（不算自己和1）有22个数字。

3.三角恒等式

对称性恒等式

$$\sin(-\theta)=-\sin(\theta), cos(-\theta)=cos(\theta),\tan(-\theta)=-tan(-\theta),\\ \sin(\frac{\pi}{2}-\theta)=\cos(\theta), \cos(\frac{\pi}{2}-\theta)=\sin(\theta),\tan(\frac{\pi}{2}-\theta)=\cot(\theta)$$

毕达哥拉斯恒等式

这是由勾股定理推算出来的。

$$\sin^2\theta+\cos^2\theta=1, 1+\tan^2\theta=\sec^2\theta, 1+\cot^2\theta=\csc^2\theta$$

和或差恒等式

$$\sin(a+b)=\sin(a)\cos(b)+\cos(a)+\sin(b)\\ \sin(a-b)=\sin(a)\cos(b)-\cos(a)+\sin(b)\\ \cos(a+b)=\cos(a)\cos(b)-\sin(a)+\sin(b)\\ \cos(a-b)=\cos(a)\cos(b)+\sin(a)+\sin(b)\\ \tan(a-b)=\frac{\tan(a)+\tan(b)}{1-\tan(a)\tan(b)}\\ \tan(a-b)=\frac{\tan(a)-\tan(b)}{1+\tan(a)\tan(b)}$$

背诵的时候，只需要记住一半，其他的是符号相反。

等腰三角形恒等式

其实就是和或差恒等式公式里面a=b的情况下，推导出来的。

$$\sin(2\theta)=2\sin(\theta)\cos(\theta)$$

在阅读Detour源码里面有这样的应用。里面将会读取一个sin cos的一半做乘法。

$$\cos(2\theta)=\cos^2(\theta)-\sin^2\theta=2\cos^2(\theta)-1=1-2\sin^2(\theta)$$ $$\tan(2\theta)=\frac{2\tan(\theta)}{1-\tan^2\theta}$$

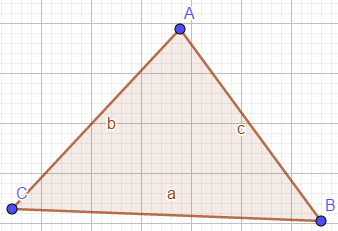
正弦、余弦定理

如果已知边长，已知角度，需要推算出未知边长度，就需要使用这个定理。而且是任意三角形。

• 正弦定理

$$\frac{\sin(A)}{a}=\frac{\sin(B)}{b}=\frac{\sin(C)}{c}$$

• 余弦定理

$$a^2=b^2+c^2-2bc\cos(A)\\ b^2=a^2+c^2-2ac\cos(B)\\ c^2=b^2+b^2-2ab\cos(C)$$

3.向量

向量计算应用于游戏中来计算位置，里面和三角函数也有关系。

向量和标量不一样，

标量(scale)只表示数值大小；

向量(矢量、vector)包含方向和数值大小。

举例：

速度、位移是向量

速率、长度是标量

零向量是指的长度为0，无方向的向量。

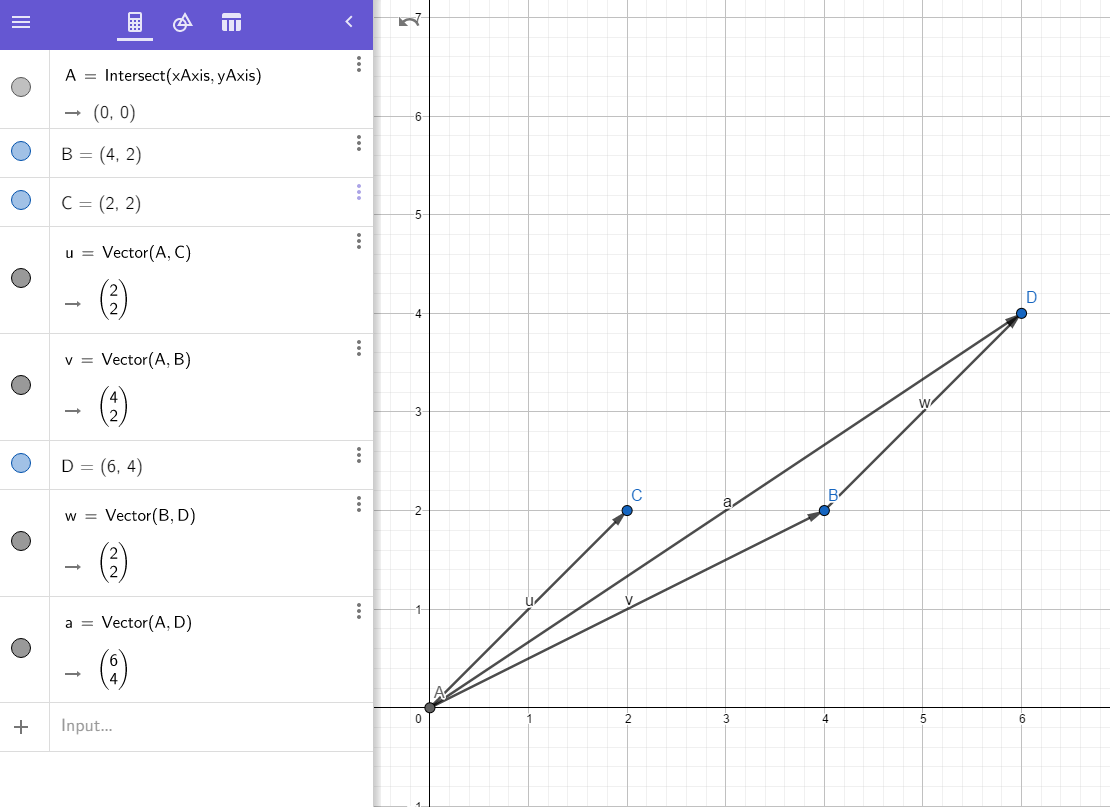
1.加法

将两个向量拼接成平行四边形，对角向量就是加法的结果。两个相同的向量相加，等于将向量长度增加一倍。

$$\vec{u} + \vec{v} = \vec{a}$$

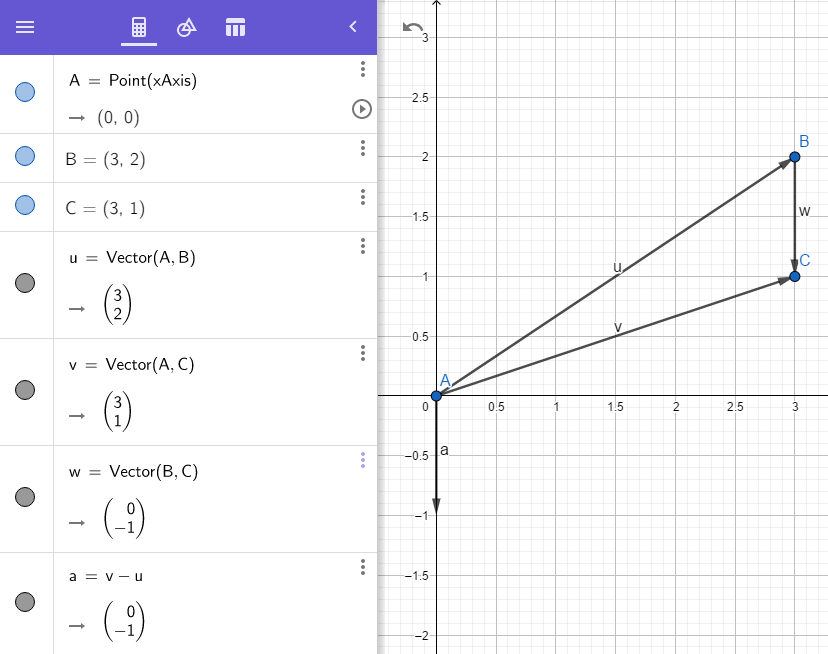
2.减法

u向量-v向量，就是指的从u向量目的点指向v向量目标点

$$\vec{v} - \vec{u} = \vec{w} = \vec{a}$$

3.向量与标量乘

向量与标量乘法，将向量按照某个长度缩放，一般用于单位向量向前行进、缩回多少距离。

4.获取长度

获取向量从开始到结束的距离。从向量得到标量。利用勾股定理，向量记录的就是直角三角形斜边在x,y轴上的投影长度，斜边长度就是x,y的平方和的开方。

数学公式里面向量长度使用双竖线引用。

$$\left||\vec{v}\right||=\sqrt{a^2+b^2}$$

5.normalized

归一化需要将向量长度计算出来，然后将向量在各个维度的分量都除以长度。这样就能得到一个单位向量。归一化用一条竖线。

$$\vec{v}_{norm} = \frac{\vec{v}} {\left||\vec{v}\right||}$$

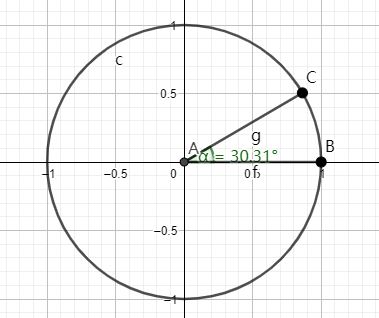
单位化的向量分量的几何意义

$$x=\cos(\theta)$$ $$y=\sin(\theta)$$

这个特性将会应用于计算位置。

6. Dot Product

$$\cos\theta=\frac{\vec{u} \cdot \vec{v}} {\left||\vec{u}\right||\left||\vec{v}\right||}$$

点乘能计算两向量的夹角的cos值。cos有一个特点，在取值±90°的值域都是>0。在游戏中，这种计算能很快判断一个怪物是否在玩家身后。这个函数不能判断左右，但是能判断前后。

7.cross produce

$$\sin\theta=\frac{\vec{u} \times \vec{v}} {\left||\vec{u}\right||\left||\vec{v}\right||}$$

叉乘用于算左右。sin有个特点，取值在0~179°都是>0。用找个特点能判定向量是在自己的左边还是右边。

叉乘需要有3个维度才有意义。

$$\vec{u}\times\vec{v}=\left|\vec{u}\right|\left|\vec{v}\right|\sin(\theta)n$$

u叉乘v之后结果是sin*u、v向量的分量。n就是垂直于u、v构成平面的垂直法线向量。

3D向量叉乘

$$\left[\begin{matrix} x_1\\ y_1\\ z_1 \end{matrix}\right] \times \left[\begin{matrix} x_2\\ y_2\\ z_2 \end{matrix}\right] = \left[\begin{matrix} y_1z_2-z_1y_2\\ z_1x_2-x_1z_2\\ x_1y_2-y_1x_2 \end{matrix}\right]$$

2D向量叉乘

$$\left[\begin{matrix} x_1\\ y_1 \end{matrix}\right] \times \left[\begin{matrix} x_2\\ y_2 \end{matrix}\right] = x_1y_2-x_2y_1$$

性质：

点乘和叉乘在一起时，有限叉乘。
反交换（交换之后数值将会变成负数）

8.获取角度

将向量转换成弧度，向量无需归一化。百度百科atan2

$$\angle\theta=\arctan(y,x)$$ $$\arctan(y,x)=\begin{cases} \arctan(\frac{y}{x}), x >0\\ \arctan(\frac{y}{x}) + \pi, y\geq 0, x\le 0 \end{cases}$$

9.常用函数

// 将弧度转换成角度
float radian2angle(float radian) {
    return radian * (180.0f / mathfu::kPi);
}

// 将角度转换成弧度
float angle2radian(float angle) {
    return angle * (mathfu::kPi / 180.0f);
}

// 将向量转换成角度
float vector2angle(mathfu::Vector<float, 2> a) {
    return radian2angle(std::atan2(a.y, a.x));
}

// 角度转换成向量
void angle2vector(float angle, mathfu::Vector<float, 2>& a) {
    auto radian = angle2radian(angle);
    a.y = std::sin(radian);
    a.x = std::cos(radian);
}

// 按照角度，长度，转换一个位置
void movepos(float angle,mathfu::Vector<float,2>& rawPos, float len, mathfu::Vector<float, 2>& out) {
    mathfu::Vector<float, 2> dir;
    angle2vector(angle, dir);
    dir.x *= len;
    dir.y *= len;
    out = rawPos + dir;
}

// 输出一个向量
void outputvector(const char* tag, mathfu::Vector<float, 2>& a) {
    std::cout << tag << " "<< a.x << "," << a.y << "\n";
}

实例

1.计算围绕role的怪物

先检查是否和其他怪物重合
按照±小角度开始偏移尝试是否能站

##include "mathfu/vector.h"
##include "mathfu/constants.h"
##include <iostream>

float radian2angle(float radian) {
    return radian * (180.0f / mathfu::kPi);
}

float angle2radian(float angle) {
    return angle * (mathfu::kPi / 180.0f);
}

float vector2angle(mathfu::Vector<float, 2> a) {
    return std::atan2(a.y, a.x)*(180.0f / mathfu::kPi);
}

void angle2vector(float angle, mathfu::Vector<float, 2>& a) {
    auto radian = angle2radian(angle);
    a.y = std::sin(radian);
    a.x = std::cos(radian);
}

void outputvector(const char* tag, mathfu::Vector<float, 2>& a) {
    std::cout << tag << "=(" << a.x << "," << a.y << ")\n";
}

// rawBattleCircleFix posSelf: linmath.Vector3{X:11424.3, Y:-311.48605, Z:17336.395}, 
// posEnemy: linmath.Vector3{X:11330.254, Y:-311.48605, Z:17465.838},
// newPos: linmath.Vector3{X:11245.467, Y:-311.48605, Z:17601.525},
// angle: -32, e2sLen: 160.00067
// 测试怪物按照弧形排布在玩家周围
void test_monster_battle_cricle()
{
    float dst = 160.0f; // 怪物距离
    float bodyRadius = 80.0f;// 怪物的宽度

    mathfu::Vector<float, 2> monsterPos(11424.3f, 17336.395f);
    mathfu::Vector<float, 2> rolePos(11330.254f, 17465.838f);
    auto dir = monsterPos - rolePos;
    auto angle = vector2angle(dir) + 20.0f;

    mathfu::Vector<float, 2> finalDir;
    angle2vector(angle, finalDir);

    finalDir.x *= dst;
    finalDir.y *= dst;

    mathfu::Vector<float, 2> newPos = rolePos + finalDir;
    
    outputvector("monsterPos", monsterPos);
    outputvector("rolePos", rolePos);
    outputvector("newPos",newPos);
}

cmake定义文件

cmake_minimum_required (VERSION 3.2)
project(math_base)

IF (CMAKE_SYSTEM_NAME MATCHES "Windows")
    add_definitions(-DWIN32)
    add_definitions(-DWIN32_LEAN_AND_MEAN)
    add_definitions(-D_WINSOCK_DEPRECATED_NO_WARNINGS)
    add_definitions(-D_CRT_SECURE_NO_WARNINGS)
    add_definitions(-D_USE_MATH_DEFINES)
ENDIF (CMAKE_SYSTEM_NAME MATCHES "Windows")

include_directories( $ENV{MATHFU_PATH}/include )

file(GLOB_RECURSE all_SRC "src/*.cpp" 
    "src/*.hpp" "src/*.h" 
    "src/*.cc" )

add_executable(test_math ${all_SRC})

target_link_libraries(test_math)

计算的位置，在坐标系上的位置

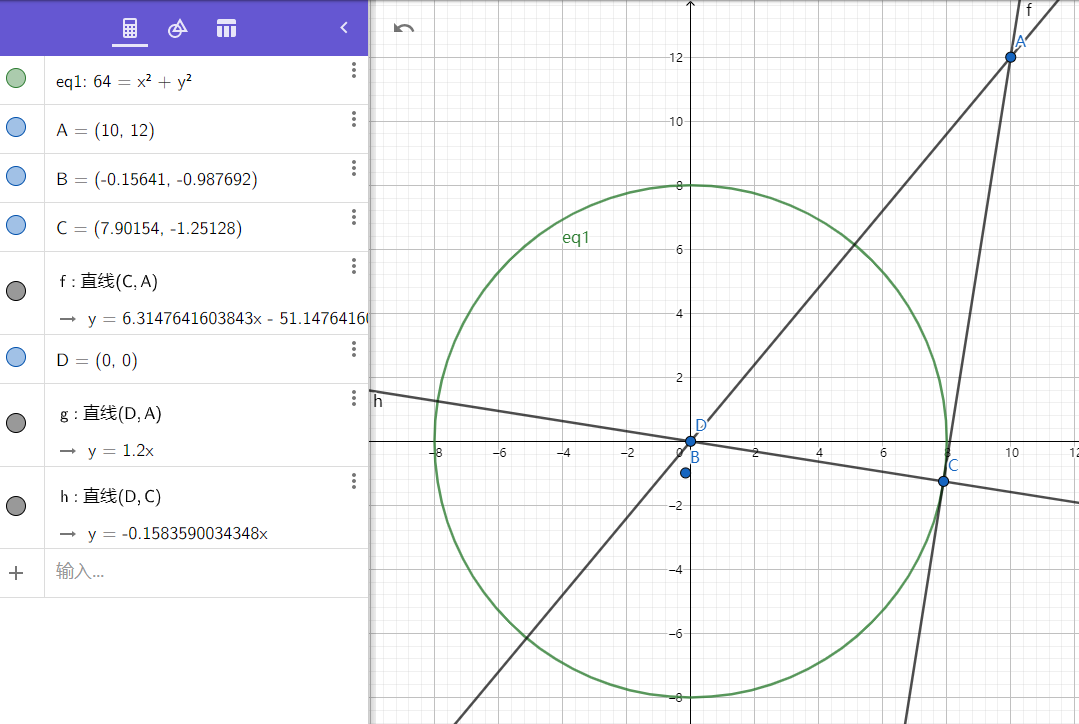
2.计算园外切线

利用三角函数来计算点对于圆的切线；

void test_fun_fix_circle()
{
    // 圆半径
    float radius = 8.0f;
    // 圆心位置
    mathfu::Vector<float, 2> circlePos(0, 0);
    // 园外一点
    mathfu::Vector<float, 2> checkPos(10, 12);
    // 园外点指向圆心向量
    mathfu::Vector<float, 2> l = circlePos - checkPos;

    // 计算距离
    auto len = l.Length();

    // 计算出园外点指向圆心向量角度
    float cos = radius / len;
    float radian = std::acos(cos);
    
    // 直角三角形，计算另一角度
    float offsetangle = 90 - radian2angle(radian);
    
    // 将园外点指向圆心向量归一化，将向量转换成角度
    auto dir = l.Normalized();
    auto oldAngle = vector2angle(l);

    // 将 园外点指向圆心向量角度 + 通过直角三角形方式计算出来的夹角
    // 这个夹角就切线方向
    auto finalAngle = oldAngle + offsetangle;

    // 将角度换算成为向量
    mathfu::Vector<float, 2> finalDir;
    angle2vector(finalAngle, finalDir);

    outputvector("finalDir", finalDir);

    // 计算出切线点离 园外点 的距离，将向量长度设置成这个距离
    auto al = std::sqrt(len * len - radius * radius);
    finalDir.x = finalDir.x * al;
    finalDir.y = finalDir.y * al;

    // 使用 园外点 + 偏移向量就能得到切线过圆边的点
    auto finalPos = checkPos + finalDir;

    outputvector("finalPos", finalPos);
}

效果：

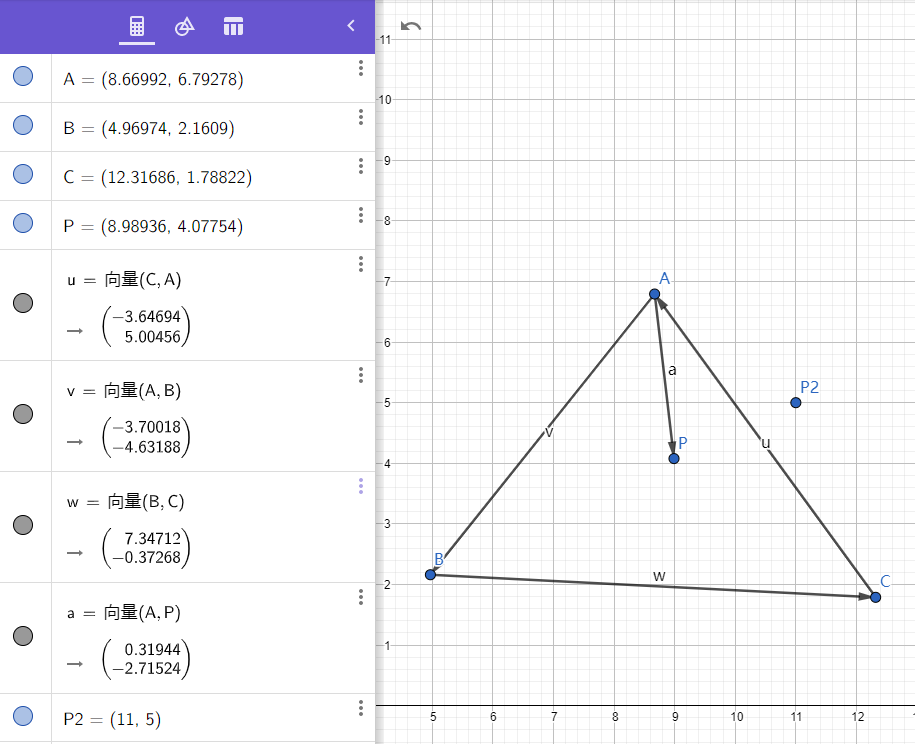
3.计算某个点是否为三角形内

原理在 b站 GAMES101-现代计算机图形学入门-闫令琪 38分钟处讲解了。

叉积是用于控制左右。如果获取的值域是正数左边，负数为右边。

利用的是，三角形三点按照顺时针的向量，以及p点的向量的叉乘永远是相同的象限的。

float cross_vector2(mathfu::Vector<float, 2>& v1, mathfu::Vector<float, 2>& v2)
{
  return v1.x * v2.y - v2.x * v1.y;
}

void test_triangle_inner()
{
  mathfu::Vector<float, 2> A(8.66992, 6.79278);
  mathfu::Vector<float, 2> B(4.96974, 2.1609);
  mathfu::Vector<float, 2> C(12.31686, 1.78822);
  mathfu::Vector<float, 2> P(8.98936, 4.07754);

  mathfu::Vector<float, 2> P2(11, 5);

  auto u = B - A;
  auto v = C - B;
  auto w = A - C;

  std::cout << "start check P\n";
  auto t = P - A;
  std::cout << cross_vector2(t, u) << "\n";
  t = P - B;
  std::cout << cross_vector2(t, v) << "\n";
  t = P - C;
  std::cout << cross_vector2(t, w) << "\n";


  std::cout << "start check P2\n";
  t = P2 - A;
  std::cout << cross_vector2(t, u) << "\n";
  t = P2 - B;
  std::cout << cross_vector2(t, v) << "\n";
  t = P2 - C;
  std::cout << cross_vector2(t, w) << "\n";
}

//output:
//start check P
//11.3947
//28.8183
//23.5922
//start check P2
//- 0.317775
//43.247
//20.8761
// 如果旋转方向相同，这些向量的sin值的符号都是一致的。
//

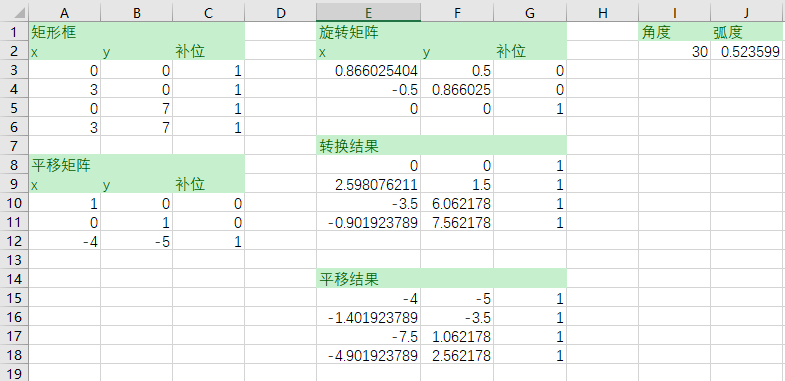
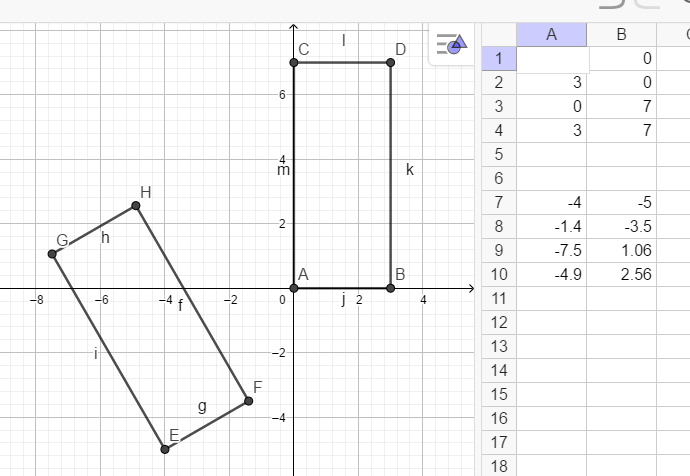
4.计算矩形内的一点

$$\begin{cases} x'=x\cos(\theta)+y\sin(\theta)\\ y'=-x\sin(\theta)+y\cos(\theta) \end{cases} \tag{4.1}$$

原理和三角形检查一样。

先将一个矩形做偏移，旋转：

取两个点开始计算：

void test_rect_inner()
{
    mathfu::Vector<float, 2> r1(-4, -5);
    mathfu::Vector<float, 2> r2(-1.401923789, -3.5);
    mathfu::Vector<float, 2> r3(-4.901923789, 2.562177826);
    mathfu::Vector<float, 2> r4(-7.5, 1.062177826);


    mathfu::Vector<float, 2> i(-4.88, -1.49);
    mathfu::Vector<float, 2> j(-8.26, -3.77);

    std::cout << "计算i点\n";
    auto t1 = r2 - r1;
    auto t2 = i - r1;
    std::cout << mathfu::Vector<float, 2>::DotProduct(t1,t2) << "\n";
    t1 = r3 - r2;
    t2 = i - r2;
    std::cout << mathfu::Vector<float, 2>::DotProduct(t1, t2) << "\n";
    t1 = r4 - r3;
    t2 = i - r3;
    std::cout << mathfu::Vector<float, 2>::DotProduct(t1, t2) << "\n";
    t1 = r1 - r4;
    t2 = i - r4;
    std::cout << mathfu::Vector<float, 2>::DotProduct(t1, t2) << "\n";

    std::cout << "计算j点\n";

    t1 = r2 - r1;
    t2 = j - r1;
    std::cout << mathfu::Vector<float, 2>::DotProduct(t1, t2) << "\n";
    t1 = r3 - r2;
    t2 = j - r2;
    std::cout << mathfu::Vector<float, 2>::DotProduct(t1, t2) << "\n";
    t1 = r4 - r3;
    t2 = j - r3;
    std::cout << mathfu::Vector<float, 2>::DotProduct(t1, t2) << "\n";
    t1 = r1 - r4;
    t2 = j - r4;
    std::cout << mathfu::Vector<float, 2>::DotProduct(t1, t2) << "\n";
}

判断点是否在矩形里面

5.计算两个角度相差

这段代码是复制unreal engine4里面的。

template< class T >
static inline T Sign(const T A)
{
    return (A > (T)0) ? (T)1 : ((A < (T)0) ? (T)-1 : (T)0);
}

void WindRelativeAnglesDegrees(float InAngle0, float& InOutAngle1)
{
    const float Diff = InAngle0 - InOutAngle1;
    const float AbsDiff = std::abs(Diff);
    if (AbsDiff > 180.0f)
    {
        InOutAngle1 += 360.0f * Sign(Diff) * std::floor((AbsDiff / 360.0f) + 0.5f);
    }
}

void test_windRelativeAngle()
{
    float a0 = 10;
    float a1 = -10;
    
    WindRelativeAnglesDegrees(a0, a1);
    std::cout << a0 - a1 << "\n";

    a0 = 10;
    a1 = 350;
    WindRelativeAnglesDegrees(a0, a1);
    std::cout << a0 - a1 << "\n";

    a0 = 370;
    a1 = 20;
    WindRelativeAnglesDegrees(a0, a1);
    std::cout << a0 - a1 << "\n";

}

大意就是将a0,a1两个角度（无论角度是不是±180°区间，这个角度是绝对角度）计算了之后，再次做减法，计算出角度为夹角度数，且夹角会保持在±180°之内。

6.角度格式化

// Utility to ensure angle is between +/- 180 degrees by unwinding.

// 将度数限制在±180°
func UnwindDegrees(A float64) (R float64) {
    for A > 180.0 {
        A -= 360.0
    }
    for A < -180.0 {
        A += 360.0
    }
    R = A
    return
}

7. 计算线段与圆相交

参考文献

#include <iostream>
#include <mathfu/vector.h>

using Vector2 = mathfu::Vector<float, 2>;

Vector2 zero = Vector2(0.0f,0.0f);

int BetweenLineAndCircle(
  Vector2 circleCenter, float circleRadius,
  Vector2 point1, Vector2 point2,
  Vector2 &intersection1, Vector2 &intersection2)
{
  float t;

  auto dx = point2.x - point1.x;
  auto dy = point2.y - point1.y;

  auto a = dx * dx + dy * dy;
  auto b = 2 * (dx * (point1.x - circleCenter.x) + dy * (point1.y - circleCenter.y));
  auto c = (point1.x - circleCenter.x) * (point1.x - circleCenter.x) + (point1.y - circleCenter.y) * (point1.y - circleCenter.y) - circleRadius * circleRadius;

  auto determinate = b * b - 4 * a * c;
  if ((a <= 0.0000001) || (determinate < -0.0000001))
  {
    // No real solutions.
    intersection1 = zero;
    intersection2 = zero;
    return 0;
  }
  if (determinate < 0.0000001 && determinate > -0.0000001)
  {
    // One solution.
    t = -b / (2 * a);
    intersection1 = Vector2(point1.x + t * dx, point1.y + t * dy);
    intersection2 = zero;
    return 1;
  }

  // Two solutions.
  t = (float)((-b + std::sqrt(determinate)) / (2 * a));
  intersection1 = Vector2(point1.x + t * dx, point1.y + t * dy);
  t = (float)((-b - std::sqrt(determinate)) / (2 * a));
  intersection2 = Vector2(point1.x + t * dx, point1.y + t * dy);

  return 2;
}

int main(int argn, char* argc[]) {
  Vector2 circleCenter(-2.84f,2.82f);
  float circleRadius = 3.5f;
  Vector2 point1(-5.48f,5.12f);
  Vector2 point2(-0.55f,5.47);
  Vector2 intersection1;
  Vector2 intersection2;
  
  int pointCount = BetweenLineAndCircle(circleCenter, circleRadius, point1, point2, intersection1, intersection2);

  std::cout << "pointCount: " << pointCount;  

  return 0;
}

8.点的旋转

4.矩阵

1.概念

$$\left|\begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{matrix}\right| \tag{A}$$

矩阵是按照行列方式排列的数字。是线性代数里面中重要的数学概念。

描述矩阵一般都是说

$$r \times c$$

的矩阵。r是rows行（横着的条目算1个），c是column（竖着的条目算1个）

方阵就是行和列数目都是相同的。在3d运算中经常使用这种方阵

单位矩阵，对角线都是1，其余都是0。

$$\left|\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}\right| \tag{M}$$

书写的时候，矩阵都是写成大写。M，A，R。手写的时候，矩阵的括号其实要写成圆括号()，印刷体中都是[]表示。

向量转换成矩阵可以成为 行矩阵、列矩阵。

2.矩阵运算

• 单位矩阵

主对角线数字都为1，其他位置都为0。

1.转置

$$\left| \begin{matrix} 1 \\ 2 \\ 3 \end{matrix}\right|\tag{M}$$ $$\left| \begin{matrix} 1 & 2 & 3\\ \end{matrix} \tag{A}\right|$$

记作：

$$M^t=A$$

2.矩阵与标量乘

$$M*k= k *\left| \begin{matrix} m11 & m12 & m13\\ m21 & m22 & m23\\ m31 & m32 & m33\\ \end{matrix} \right| = k \left| \begin{matrix} k*m11 & k*m12 & k*m13\\ k*m21 & k*m22 & k*m23\\ k*m31 & k*m32 & k*m33\\ \end{matrix} \right|$$

3.矩阵乘法

公式定义：

$$(AB)_{ij}=\sum_{k=1}^p a_{i1}b_{1j}+a_{i2}b_{2j}+...+a_{ip}b_{pj}$$

公式分解：

$$A*B= \left| \begin{matrix} a11 & a12 & a13\\ a21 & a22 & a23\\ \end{matrix} \right| * \left| \begin{matrix} b11 & b12 \\ b21 & b22 \\ b31 & b32 \\ \end{matrix} \right|=\left| \begin{matrix} a11b11+a12b21+a13b31 & a11b21+ a12b22+a13b23\\ a21b11+a22+b21+a23b31 & a21b12+a22b22+a23b32\\ \end{matrix} \right|$$ $$A*B=C$$

1、当矩阵A的列数（column）等于矩阵B的行数（row）时，A与B可以相乘。

2、矩阵C的行数等于矩阵A的行数，C的列数等于B的列数。

3、乘积C的第m行第n列的元素等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和。

在线性代数课程中，宋老师的7字口诀：

宋老师七字口诀：

$$A_{3 \times 4} B_{4 \times 5}$$

中间相等，取两头。

其实就是罗列矩阵的下标数字：

3,4,4,5

中间数字： 4,4相等，就能乘；

取两头： 3,5 这就是结果的矩阵的形状。

wps矩阵计算

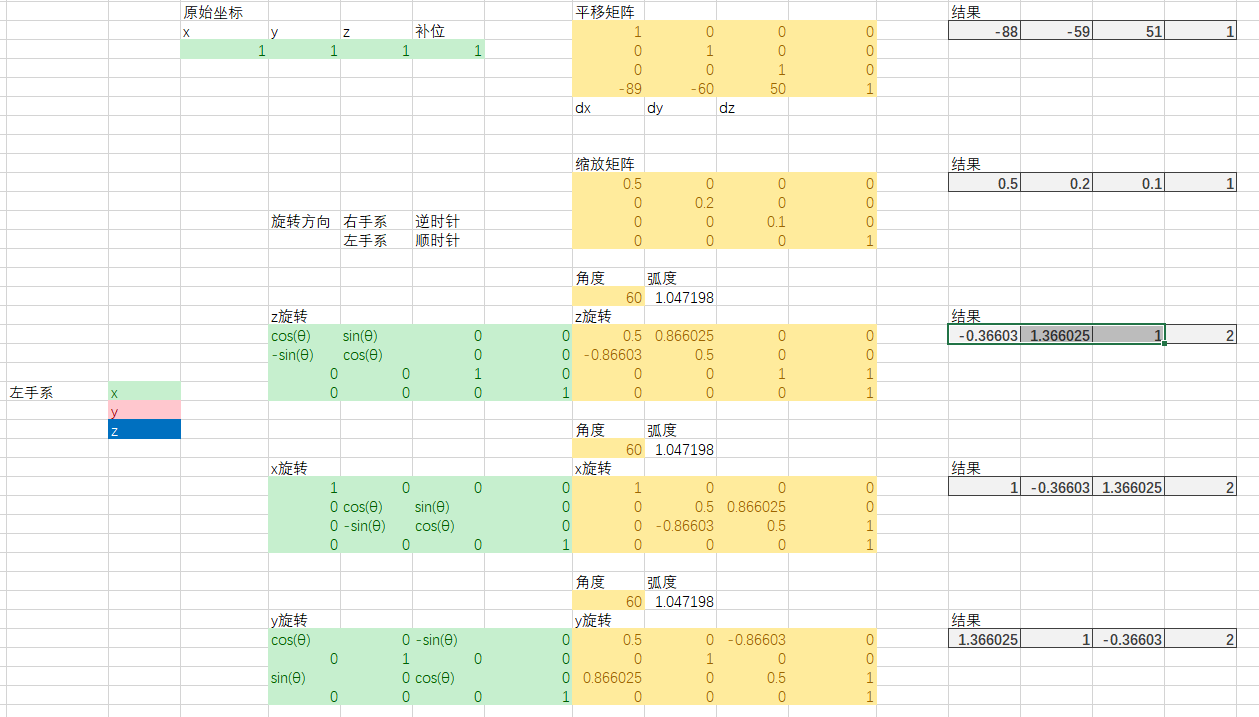
使用矩阵来做位移，旋转，缩放操作：

坐标系上的位置：

4.克罗内克积（Kronecker Product）

克罗内克积是两个任意大小的矩阵间的运算，符号记作 。克罗内克积也被称为直积或张量积.以德国数学家利奥波德·克罗内克命名。

$$\left| \begin{matrix} a11 & a12 \\ a21 & a22 \\ \end{matrix} \right| \bigotimes \left| \begin{matrix} b11 & b12 \\ b12 & b22 \\ \end{matrix} \right| = \left| \begin{matrix} a11b11 & a11b12 & a12b11 & a12b12 \\ a11b21 & a11b22 & a12b21 & a12b22 \\ a21b11 & a11b12 & a22b21 & a22b22 \\ a21b21 & a21b22 & a22b21 & a22b22 \\ \end{matrix} \right|$$

6.欧拉角

先使用左手坐标系。

摆上一个飞机，y轴指天，x轴右，z轴向前。

1. 飞机围绕着y轴旋转，叫做偏离航向（heading），偏航角（Yaw），航向角（Heading Angle）；
2. 飞机围绕着x轴旋转，叫做俯仰（pitch）调整，俯仰角（Pitch），偏斜角（Angle of Declination）；
3. 飞机围绕着z轴旋转，叫做滚转（bank）调整，翻滚角（Roll）；

4.万向节死锁

在使用欧拉角来做旋转的时候，当我们将俯仰数值调整成±90°的时候。再去调整偏航、滚转的时候，保持一致。本来有3个维度上的旋转，最后只能从两个维度上调整。

欧拉角和后面说的四元数的插值计算也是存在一些差异的。

欧拉角、四元数插值差异

插值的时候，四元数可以使用球形插值SLerp，在空间上转换的时候，会在球面上画弧线。欧拉角是按照轴来做的。

2.欧拉恒等式

我还没有理解到这个意义。

$$\cos\varphi+i\sin\varphi=e^{i\varphi}$$

当

$$\varphi=\pi$$

推导

$$e^{i\pi}+1=0$$

5.四元数

1.概述

四元数是1843年发明的。爱尔兰数学家哈密顿(William Rowan Hamilton,1805-1865）。

四元数运算在电动力学与广义相对论中有广泛的应用。四元数可以用来取代张量表示。有时候采用带有复数元素之四元数会比较容易，导得结果不为除法代数之形式。然而亦可结合共轭运算以达到相同的运算结果。

从概念上来看，就是在数学里面定义对于-1开方最后获取的值。

$$i=\sqrt{-1}$$

复数是对实数集合的一种扩展。

在游戏开发应用里面，四元数用于做旋转计算。所以最好先将矩阵搞清楚。复数已经是一种数学工具了，在实际世界里面不能表示什么意义。

四元数不是专门给3D图形学设计的，但是能用在3D图形学里面：

• [3D相机控制]
• 压缩存储
• 平滑3D插值

复数定义

$$z=a+b*i$$

a是实部，b是虚部；

复数与标量相乘、相除

$$k*Z_{1}=k*(a+bi)=k*a+(k*b)*i$$

复数加减

$$Z_{1}=(a+b*i)$$ $$Z_{2}=(c+d*i)$$ $$Z_{1}+Z_{2}=(a+b*i)+(c+d*i)=((a+c)+(b+d)*i)$$ $$Z_{1}-Z_{2}=(a+bi)-(c+di)=(a-c)+(b-d)i$$

复数加法恒等元

复数恒等元

$$(0+0*i)$$

复数除法

$$Z_{1}/Z_{2}=\frac{(a+b*i)}{(c+d*i)}$$

推算的时候，需要分子和分母都乘上分母的共轭复数。

共轭(Conjugate)

两个实部相等，虚部互为相反数的复数互为共轭复数(conjugate complex number)。（当虚部不等于0时也叫共轭虚数）复数z的共轭复数记作 （z上加一横，英文中可读作Conjugate z,z conjugate or z bar），有时也可表示为

$$Z^*=\overline{Z}$$ $$Z=(a+bi)$$ $$\overline{Z}=(a-bi)$$

计算负数的模

$$\left||p\right||=\sqrt{p\overline{p}}$$

中划线

$$\underline{\text{下划线}}$$ $$\overline{\text{上划线}}$$

参考

• [1] markdown公式
• [2] windows10输入公式
• [3] 三角函数
• [4] 图形计算器
• [5] GeoGebra 数学
• [6] GeoGebra-Classic
• [7] Google-mathfun库
• [8] GAMES101-现代计算机图形学入门-闫令琪
• [9] NumPy教程
• [10] 2d/3dPython库
• [11] markdown公式2
• [12] markdown公式3
• [13] B站矩阵
• [14] 极坐标
• [15] 3d数学笔记
• [16] 妈咪说-复数
• [17] GeoGebra-Classic-Win版本
• [18] 复数运算规则
• [19] 欧拉角和四元数的理解
• [20] 欧拉角和万向节死锁
• [21] 万向节死锁实例
• [22] 在线LaTex工具
• [23] 3D数学基础图形与游戏开发-视频