简介
阅读算法导论之后做的读书笔记。在第二部分,第6章。
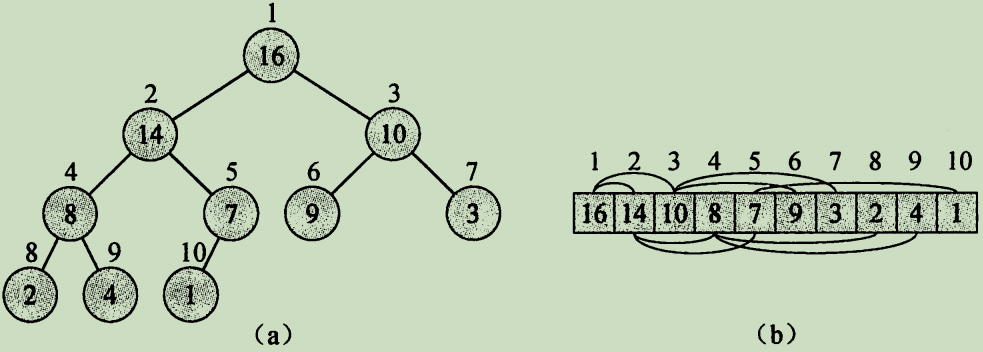
堆其实是近似的完全二叉树。一般都是通过数组来存储。
排序过程
- 建堆:目的就是将无须的堆,将最大的数字挑出来放到队列首部;
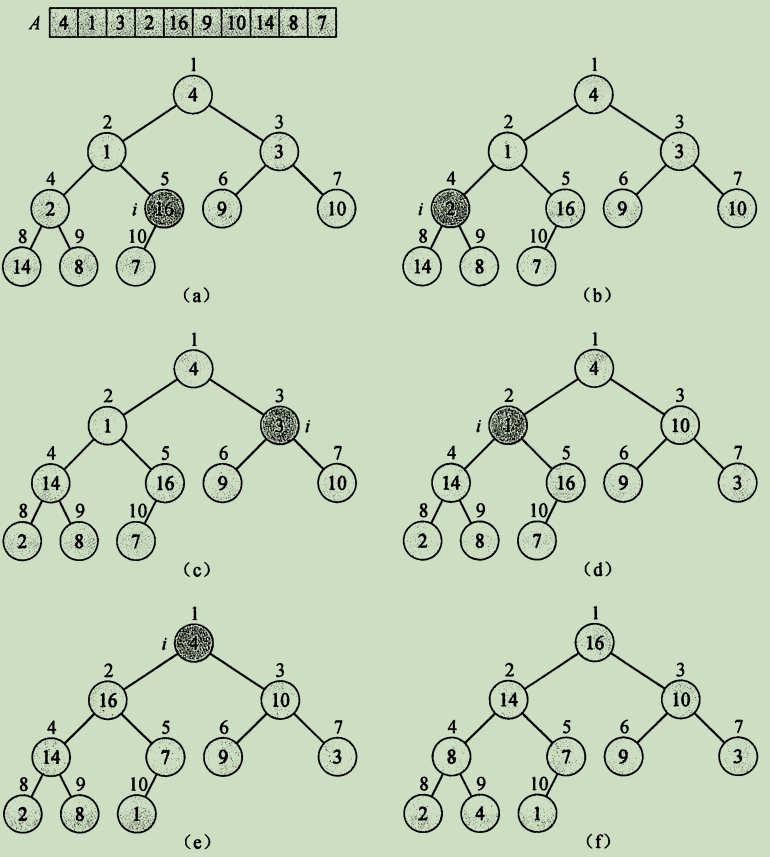
- 将堆顶元素取出放到数组尾部,将堆元素减少一个;
- 重新对堆进行排序;
如果是最大堆,那就意味着父节点需要比子节点大。如此循环计算,直到树上的节点都符合这个规则。
源代码
github
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
| ##include <stdio.h>
##include <stdlib.h>
##include <time.h>
##include <string.h>
int MAX_ARRAY = 10;
int NUMBER_RANGE = 100;
int* raw_array = 0;
void init_rand_env()
{
srand((unsigned)time(0));
}
void rand_array_number()
{
int i;
for (i = 0; i < MAX_ARRAY; i++)
raw_array[i] = rand() % NUMBER_RANGE;
}
void output_array()
{
int i;
for (i = 0; i < MAX_ARRAY; i++)
printf("%d ", raw_array[i]);
printf("\n");
}
int left(int i)
{
return (i + 1) * 2 - 1;
}
int right(int i)
{
return (i + 1) * 2;
}
void max_heapify(int* A, int size, int i)
{
int l, r, largest,tmp;
l = left(i);
r = right(i);
if (l < size && A[l] > A[i])
largest = l;
else
largest = i;
if (r < size && A[r] > A[largest])
largest = r;
if (largest != i) {
tmp = A[i];
A[i] = A[largest];
A[largest] = tmp;
max_heapify(A, size, largest);
}
}
void build_max_heap(int* A, int size)
{
int i;
for (i = (size+1)>>1; i > 0; ) {
--i;
max_heapify(A, size, i);
}
}
void heap_sort(int* A, int size)
{
int i,tmp;
build_max_heap(A, size);
printf("C make heap finish\n");
output_array();
for (i = size-1; i > 0; i--) {
tmp = A[0];
A[0] = A[i];
A[i] = tmp;
size--;
max_heapify(A, size, 0);
output_array();
}
}
int main(int argn, char* argc[])
{
if (argn != 3)
{
printf("usage: test_heapsort MAX_ARRAY NUMBER_RANGE\n");
return -1;
}
MAX_ARRAY = atoi(argc[1]);
NUMBER_RANGE = atoi(argc[2]);
init_rand_env();
raw_array = (int *)malloc(sizeof(int) * MAX_ARRAY);
rand_array_number();
output_array();
heap_sort(raw_array, MAX_ARRAY);
output_array();
free(raw_array);
return 0;
}
|
应用场景
libevent最小堆
在libevent源码中能看到它们的定时器是使用的最小堆来实现的。minheap-internal.h代码一共193行。定时器逻辑,是按照时间来排序一堆节点,将到期的节点将会被pop出来,这个场景下,建堆过程就比较轻松。
数据结构
1
2
3
4
5
6
7
|
typedef struct min_heap
{
struct event** p;
unsigned n, a;
} min_heap_t;
|
工具函数
min_heap_elem_greater(a, b) 比较两个节点的大小。
min_heap_ctor_ 清理堆的成员;
min_heap_dtor_ 释放堆的内存块;
min_heap_elem_init_ 堆元素的初始化;
min_heap_empty_ 堆是否为空;
min_heap_size_ 堆的大小;
min_heap_top_ 获取堆顶元素;
min_heap_elt_is_top_ 检查某个节点是否为堆顶;
1
2
3
4
|
unsigned parent = (e->ev_timeout_pos.min_heap_idx - 1) / 2;
min_child = 2 * (hole_index + 1);
|
操作函数
min_heap_push_ 将元素入堆。
1
2
3
4
5
| 总分配元素个数是否太多,否则不给分配。
检查容积是否足够,否则用realloc将内存扩大分配。分配时,a如果为0就直接初始化成8,每次都是a*2来分配内存。[8,16,32,64,128,512,...]。`int min_heap_reserve_(min_heap_t* s, unsigned n)`
调用函数,将堆开始排序`min_heap_shift_up_`。
|
min_heap_shift_up_ 插入堆。
1
2
3
4
5
6
| 读取堆最末尾的一个节点的parent。
如果当前位置不是根位置,而且父节点>插入来的新节点;
将父节点的信息写入到子节点,修改父节点位置idx;
将当前位置赋值为父节点位置;
退出循环之后将算出来的位置填充成输入的新节点;
|
min_heap_pop_ 弹出堆。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| 检查对是否为空。
读取顶部元素。
将堆数量减少,调用`min_heap_shift_down_`函数将顶部元素清理掉。
将顶部元素index设置成-1。
`void min_heap_shift_down_(min_heap_t* s, unsigned hole_index, struct event* e)` 删除堆中指定位置的元素,将e元素插入到子树中,让子树保持堆规律。
计算出此节点的右子节点位置。
如果子节点位置还在树里面开启循环:
如果刚好子树时最后一个子树,直接拿左子树
或者右子树大于左子树时,拿左子树
否则拿右子树
(这三个步骤为了拿到最小的子树节点)
找出来的子树里面最小节点,和输入的e相比,e还小一些,将退出循环
否则,将检查点设置成拿到的最小子树节点,将子树节点设置上parent节点。
将hole_index设置成最小子树节点位置;
读取最小子树节点的子节点位置,开始下一轮检查;
退出循环后,将找出来的hole_index填写上输入的位置。
|
int min_heap_erase_(min_heap_t* s, struct event* e) 将堆中e元素删除掉
1
2
3
4
5
6
7
| 检查e是否为有效的元素,无效将会不处理;
读取最后一个节点,将堆的size减少1;
计算当前节点的父节点位置;
* 我们使用last元素替换掉e位置的元素。如果last小于e的父节点将使用往上找插入点,如果大于一个或两个子节点将往下找。当子节点都小于父节点,它将无需向上或者向下找。
如果节点位置不是根,而且这个节点的父节点比最后一个节点要大将进入`min_heap_shift_up_unconditional_`处理
否则就是开始向下找合适的位置替换`min_heap_shift_down_`,类似删除根节点的处理操作;
将摘除的节点设置成无效节点;
|
min_heap_shift_up_unconditional_ 插入的数据e要小于hole位置父节点,所以它需要往上找插入点。
1
2
3
4
5
6
| 先计算父节点位置,开始循环
将hole父节点移植到hole位置。
将hole变量设置成parent位置。
开始计算hole的parent位置。
当hole不是根,而且parent位置是大于e会继续执行循环
将找到的hole位置填充上e变量。
|
min_heap_adjust_ 将一个元素e适配到堆合适的位置,将变量数值调整了,让其能正确的放到一个位置。
1
2
3
4
5
| 如果是无效的位置,直接走`min_heap_push_`流程。
如果是在堆里元素
获取父节点
计算此节点是否子节点,而且父节点大于自己,将调用`min_heap_shift_up_unconditional_`
否则调用`min_heap_shift_down_`往下找插入点
|
STL中堆的实现(未完)

